User derivatives¶
It is possible to add additional constitutive equations to the equation of motion
This can be used to deal with multiphysics problem involving electrical circuits, pneumatics, hydraulics, …
The additional state equations will be added to the set of mechanical equations
In practice
The user must declare the state in a user model
The user must compute the state derivative equation in the user_Derivatives function
The state value can be accessed in any user function of the project
Back to the spring-pendulum example¶
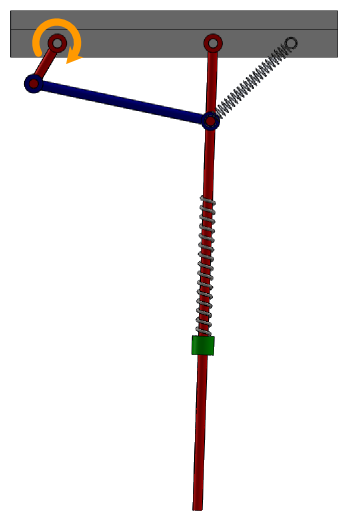
Pendulum spring illustration with torque¶
The exercise consists in adding an electrical DC motor to the pendulum example without the wall:
The motor will be connected to the revolute joint of the crank
The motor obeys the following relation
Electrical circuit equation: \(U_{mot} = R_{mot}*i_{mot}+k_{\phi}*\omega_{mot} + L \frac{di_{mot}}{dt}\)
Torque equation: \(T_{mot} = k_{\phi} * i_{mot}\)
A reductor is inserted between the motor and the axle: \(\begin{matrix} T_{axle} = \rho * T_{mot}\\ \omega_{axle} = \omega_{mot}/\rho \end{matrix}\)
The parameter values are:
\(U = 48\ V\)
\(k_{\phi} = 48.6\ mNm/A\)
\(\rho = 200\)
\(R_{mot} = 4.49\ \Omega\)
\(L = 0.573\ mH\)
Step 1: Draw your multibody system¶
Open the PendulumSpring model in MBsysPad
Add a user model for the motor
Add a scalar variable for each parameter
Add a state variable for the current
Set the nature of the :
crank joint to independent;
pendulum joint to dependent;
If you had modified the joint nature in the code in the previous section you have to update the code, modifications done in MBsysPad are overwritten.
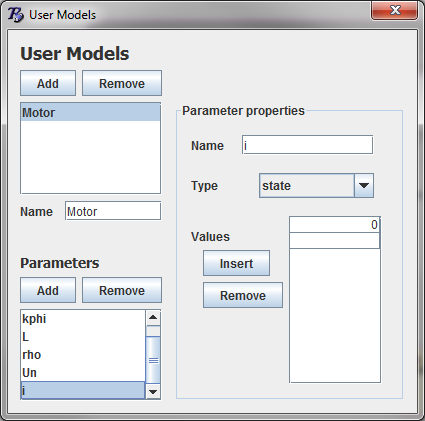
snapshot of the user model gui for introducing state variable¶
REMARK
Several state variables can be introduced either by introducing several values for a single state variable (state vector) or by defining several parameters with “state” type.
WARNING:
You can have two state variables with the same name in two different user model. However it is recommended to set an unique name for each state variable.
Step 3: Write your user function¶
Edit the user_Derivatives function and introduce the state equation for the current:
function [uxd] = user_Derivatives(ux,mbs_data,tsim)
%...
id_crank = mbs_get_joint_id(MBS_info, 'R2_crank');
um = mbs_data.user_model.Motor;
omMot = -mbs_data.qd(id_crank)*um.rho;
iMot = ux(1);
uxd(1) = (um.U-um.Rmot*iMot-um.Kphi*omMot)/um.L;
%...
REMARK:
The user state vector is accessed via the ux field of the mbs_data structure.
WARNING:
The ID of a state variable cannot be retrieved by a matlab function. The ID has to be manually determined.
Edit the user_JointForces function and introduce the torque equation:
function [Qq] = user_JointForces(mbs_data,tsim)
%...
id_crank = mbs_get_joint_id(MBS_info, 'R2_crank');
iMot = mbs_data.ux(1);
um = mbs_data.user_model.Motor;
Qq(id_crank) = -um.rho*um.Kphi*iMot;
%...
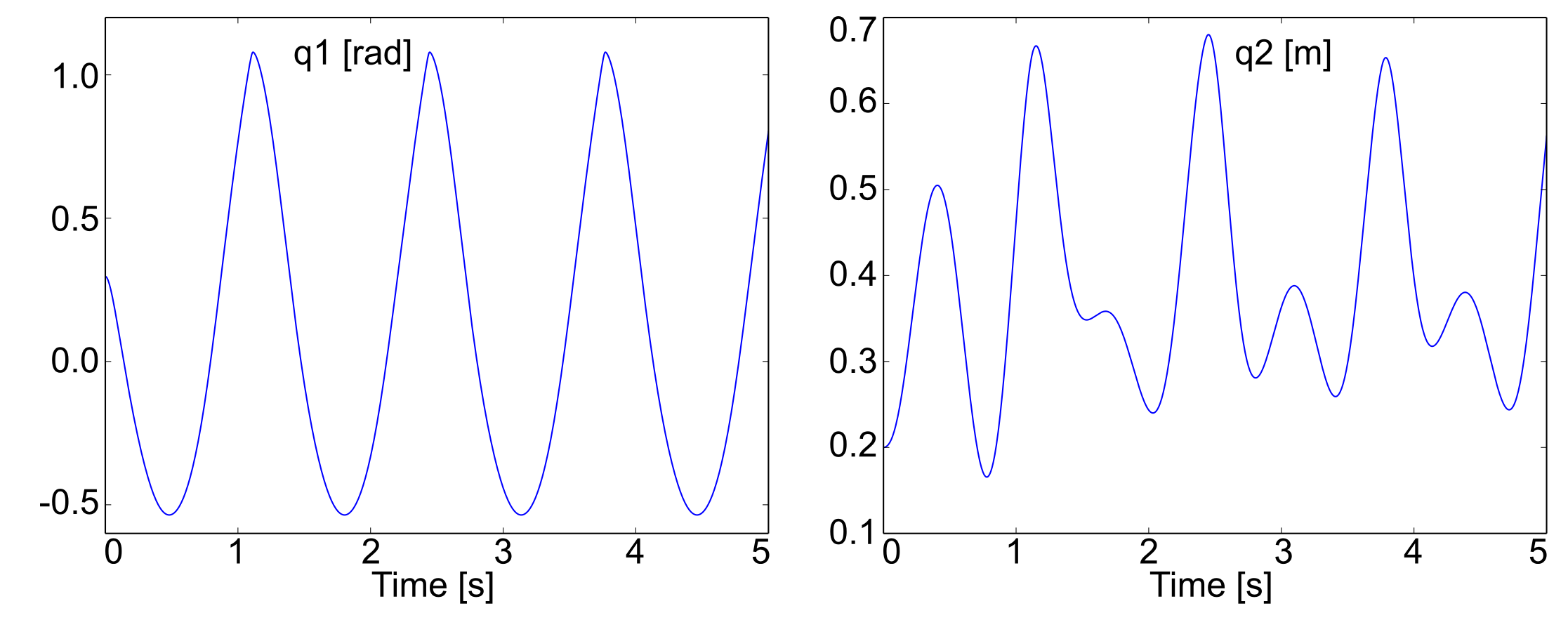
The time history of the motor current can be directly plotted from the ux field of the mbs_dirdyn structure.
REMARK:
To let the motor rotate freely, the wall must be removed (by modifying the external forces).
REMARK:
The resolution of the motor dynamics requires a smaller time step than before. The computation time will increase.